This article continues Milliman’s series on long-term care (LTC) first principles modeling. The first article in the series, released in March 2016, introduced the topic and set the stage for the series of case study discussions that would follow. The second article in the series, released in June 2016, examined the development of mortality assumptions for use in an LTC first principles model. This article discusses the issues related to developing lapse assumptions.
Our previous articles discussed the nuances of developing first principles assumptions and different approaches that can be used to build a first principles model. In this article, we examine in more detail the issues relating to developing healthy life lapse rates. As noted throughout, the common assumption that the ultimate total life lapse rate reaches a constant level produces an increasing healthy life lapse rate by duration. Alternatively, if the healthy life lapse rate remains constant once it reaches an ultimate level, that would imply that the total life lapse rate continues to decrease over time. This article also examines how mortality and lapse assumptions interact and the importance that developing an appropriate mortality assumption can have on setting lapse rate assumptions.
Choosing an approach
Legacy models for LTC business have often used total life lapse and mortality assumptions in which status (healthy versus disabled) is not necessarily tracked and the same lapse and mortality assumptions apply to all lives regardless of status. By contrast, many first principles models track policyholder status. In some first principles models, policyholders are classified as either “healthy” or “disabled.” Others allow for more sophisticated tracking of status, such as healthy, disabled (often for multiple care situs), or healthy following claim recovery, and may even track transitions between care situs. Models that track policyholder status allow for a more refined approach to modeling lapse and mortality in which separate mortality assumptions are applied to healthy lives and disabled lives as well as only applying lapse assumptions to healthy lives. Our second article on first principles modeling discussed the nuances of developing healthy and disabled life mortality.
In general, lapse assumptions can be expressed on two different bases—a healthy life basis and a total life basis. For a first principles model, the lapse assumption should be restated from a total life basis to a healthy life basis. While it is possible to develop healthy life lapse assumptions before developing healthy and disabled life mortality assumptions, we have found that developing mortality assumptions first, and then developing lapse assumptions, may allow for the observation of more logical, smooth patterns in the lapse data. Accurate coding, as much as possible, of actual deaths and benefit exhaustions, along with a representative mortality assumption, will lead to much better healthy life lapse rate assumptions. An example follows later in this article.
There are three approaches that are commonly used for developing first principles lapse assumptions. The approaches differ with respect to how mortality is handled and whether the lapse assumption is directly developed or “backed into.” Combinations of the approaches are possible as well. The three approaches can be described as follows:
1. Develop healthy life lapse assumptions directly from experience, where healthy life lapses are equal to total healthy life terminations minus actual healthy life deaths.
2. Develop a healthy life lapse assumption directly from experience by using an assumed healthy life mortality rate and the total, healthy life terminations.
3. Develop a healthy life lapse assumption on an implied basis by using total life lapse assumptions and healthy life and disabled life mortality assumptions. This approach requires a projection of the runout of lives instead of being based on an experience study. The implied lapse rate is equal to the calculated implied lapses divided by healthy lives.
In all three cases, it is assumed that mortality assumptions have already been split into healthy and disabled life assumptions. The first two approaches require an experience study to be conducted while the third merely develops healthy life lapse rates on an implied basis. Healthy life terminations refer to only those policy terminations that occur while an insured is in a healthy life status. Thus, if a policy dies while on claim or exhausts benefits, those terminations would not be considered a healthy life termination. Some of the nuances of conducting a lapse study are discussed later in this article.
The first approach is probably the most consistent with the objectives of a first principles model. The approach requires a lapse study to be conducted to directly observe healthy life lapses. The key to this approach is to accurately identify actual healthy life deaths, thereby observing healthy life lapses. Any miscoding of deaths will result in incorrect lapses. Also, exposure needs to be split into the period of time that an individual is in a healthy life status versus a disabled life status. The main advantage of this approach is that healthy life lapse rates can be directly observed. This advantage is offset by the possible lack of credible data or miscoding of deaths.
The second approach is similar to the first, except that, instead of actual healthy life deaths, assumed healthy life mortality is used. In this approach, healthy life lapse is equal to healthy life total terminations minus an assumed healthy life mortality rate. This approach is commonly done when there is some uncertainty around the accuracy of the classification of deaths. One advantage of using an assumed healthy life mortality assumption is that it will produce smoother implied lapse rates, assuming that the mortality assumption has itself been properly fit to the experience data. An example demonstrating the importance of appropriately fitting the mortality assumption before using it in the development of a lapse assumption follows later in this article. Often the actual data may not be fully credible in the later durations and ages, causing variability in observed mortality. The variability would then flow into the observed lapse rates. Using an assumed mortality assumption would smooth that out. The key to this approach is having a valid healthy life mortality assumption.
The third approach develops healthy life lapse assumptions on a theoretical basis. An experience study would not be used directly. Instead, a first principles model, using as input total life lapse assumptions and healthy life and disabled life mortality assumptions, would be used as a starting point. Lapses would be output from the model and healthy life lapse rates would be developed by dividing lapses by healthy life exposure. While this approach would maintain consistency with other assumptions, it has several disadvantages. First, the implied healthy life lapse rates would not be directly grounded in observed experience. Second, the level of granularity of the lapse assumption would be greatly expanded beyond what most companies currently use. Any place where the underlying morbidity or mortality varies would cause a unique set of implied lapse rates. This would likely not be workable for most companies, requiring the need to aggregate the lapse assumptions to a higher level. We discussed a similar challenge with respect to mortality in the prior article regarding mortality assumptions.
In all these approaches, it is important as a last step to compare actual healthy life policy terminations with the expected healthy life mortality and lapse assumptions. This final check will help verify that, when all the assumptions are brought back together, they maintain a reasonable relationship in total to the actual experience.
The following sections highlight, through use of examples, some important considerations in developing lapse rates. The first example discusses differences between healthy life and total life lapse assumptions. The second illustrates the importance of mortality in developing lapse assumptions.
Example 1: Difference between total life and healthy life lapse rates
It is a common assumption in the industry that lapse rates reach an ultimate level and stay constant at that level. For example, a typical assumption is that lapse rates start at 6%, grade down to 1% by duration 5, and then stay constant at 1% thereafter. The assumption that lapse rates reach an ultimate level cannot hold under both a total life and healthy life basis. Because only healthy lives are subject to voluntary lapse, the proportion of the total population that is healthy affects the relationship between total life lapse and healthy life lapse. Over time, as more of the total life population becomes disabled, healthy life lapse rates start to increase above the total life basis when the lapse rate is assumed to reach an ultimate level on a total life basis. Take a simple example. Say 10 policies lapse out of a total life population of 1,000 policies. The total life lapse rate is 1% (10 divided by 1,000). If 50 of the policies are on claim, that leaves 950 in a healthy life status. In that example, the healthy life lapse rate would be 1.05% (10 divided by 950). Later on, as more of the population becomes disabled, the healthy life lapse rate will increase. For example, consider that 200 of the policies are on claim, leaving 800 in a healthy life status. In that situation, the healthy life lapse rate would be 1.25% (10 divided by 800), relative to the aforementioned 1% total life lapse rate. As the mix of lives shifts toward more disabled than healthy lives, assuming the total life lapse rate stays constant, the healthy life lapse rate will increase over time.
Another example illustrates the difference between total life lapse rates and healthy life lapse rates. The morbidity assumptions are from Milliman’s 2014 Long-Term Care Guidelines. Total life lapse rates are assumed to start at 6%, grade down to 1% by duration 5, and then stay constant after that point. Similar cells or assumptions would produce a similar pattern. Figure 1 shows, for a 60-year-old woman, that the healthy life lapse rate increases over time if the total life lapse rate is assumed constant.
Figure 1: Total vs. healthy lapse rate: Female, Issue Age 60
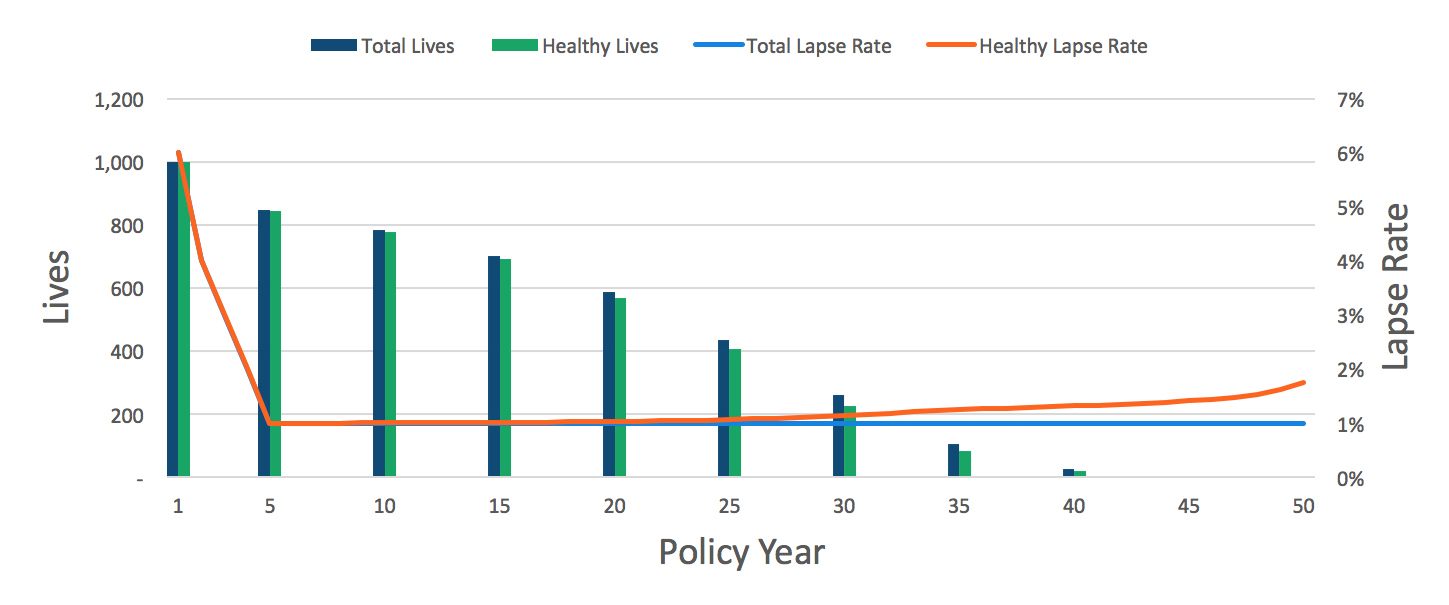
A similar example could be created where the healthy life lapse rate is assumed constant starting in duration 5. In that situation, the total life lapse rate would decrease over time, though in both cases a material divergence in lapse rates does not occur until the later policy years and older ages.
Example 2: The importance of mortality rates in developing a lapse assumption
This example illustrates the importance of using an appropriate mortality assumption when the second approach from above is used to develop a lapse assumption—that is, when lapse rate assumptions are developed by first calculating total healthy life policy termination rates and then removing assumed deaths and, when relevant, shock lapses, to arrive at an implied lapse rate.
Calculation of voluntary lapse rates in this fashion can be an effective technique for setting assumptions. However, it requires and relies upon the existence of a reasonable and appropriate mortality assumption. If the mortality assumption does not fit the historical data well, the resulting implied lapse rates will necessarily be imperfect and may exhibit unusual or unexpected patterns. The following example illustrates this point.
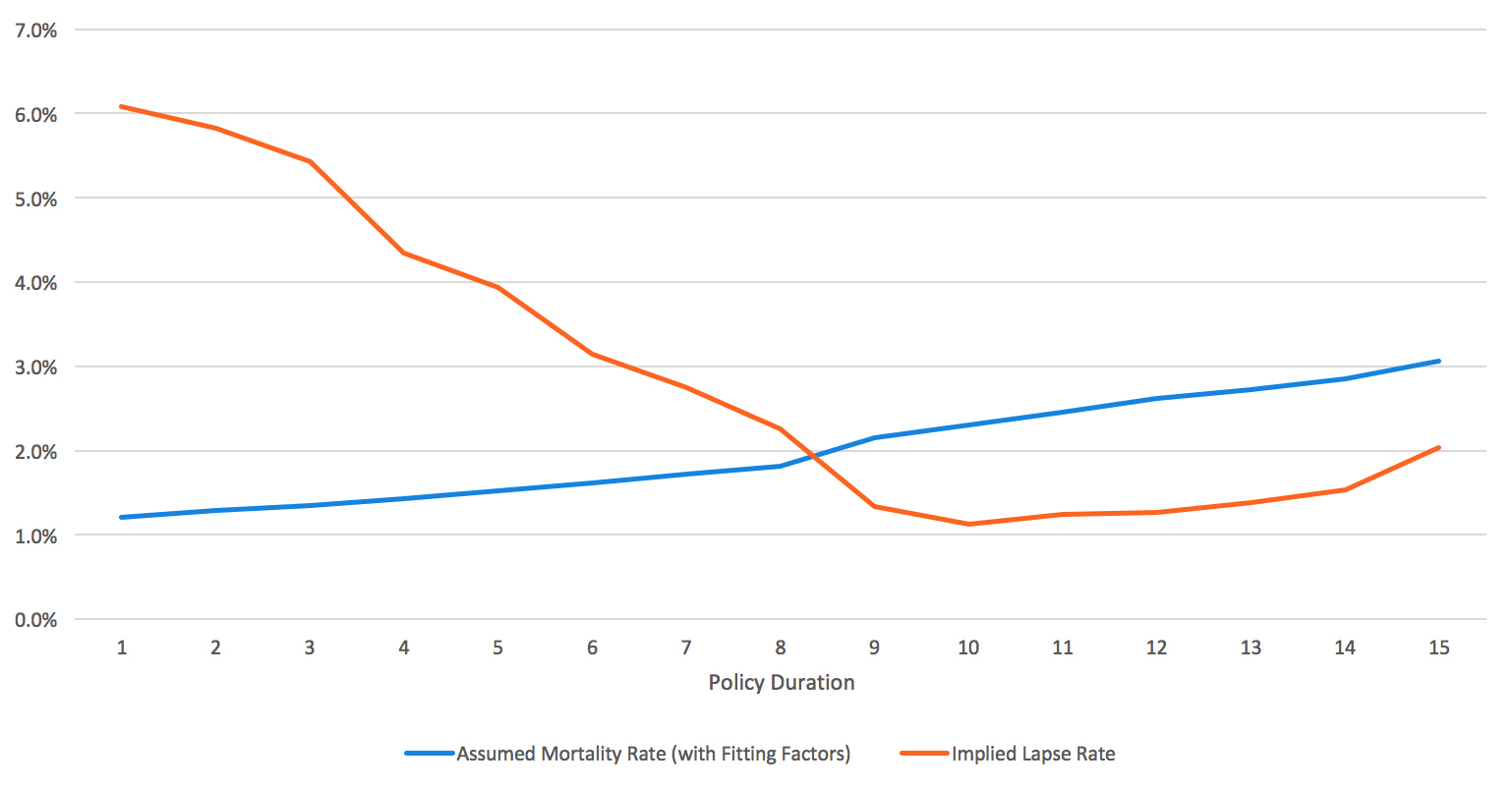
Figures 2 and 3 show the results of a lapse study in which the assumed mortality does not fit the historical experience well. The mortality assumption is based on a commonly used industry table (GAM 94), which has been adjusted in aggregate to fit the historical experience—i.e., an aggregate mortality scalar has been applied such that total expected deaths are consistent with total actual deaths. However, the mortality assumption has not been adjusted to reflect durational and attained age trends.
Figures 2 and 3 show an unexpected pattern in implied lapse rates. During the early policy durations, lapse rates steadily decline. However, the implied lapse rates reach a minimum around duration 10 after which they begin to increase steadily and materially. Using a common industry table (without durational and attained age adjustments) could, therefore, lead the actuary to conclude that lapse rates increase in late durations.
Figure 2: Long-term care lapse example Generic Lapse Study
| Duration | Exposure | Expected deaths | Benefit exhaustion | Implied lapse | Total termination |
Results Mortality rate |
Resulting lapse rate |
| 1 | 10,000 | 120 | 0 | 609 | 729 | 1.2% | 6.1% |
| 2 | 9,307 | 120 | 0 | 543 | 663 | 1.3% | 5.8% |
| 3 | 8,623 | 117 | 0 | 468 | 585 | 1.4% | 5.4% |
| 4 | 8,183 | 118 | 0 | 355 | 473 | 1.4% | 4.3% |
| 5 | 7,785 | 119 | 0 | 306 | 425 | 1.5% | 3.9% |
| 6 | 7,430 | 120 | 0 | 233 | 354 | 1.6% | 3.1% |
| 7 | 7,086 | 122 | 0 | 195 | 317 | 1.7% | 2.7% |
| 8 | 6,721 | 122 | 0 | 152 | 274 | 1.8% | 2.3% |
| 9 | 6,418 | 138 | 0 | 86 | 224 | 2.1% | 1.3% |
| 10 | 6,143 | 142 | 0 | 69 | 211 | 2.3% | 1.1% |
| 11 | 5,831 | 143 | 0 | 72 | 216 | 2.5% | 1.2% |
| 12 | 5,543 | 145 | 13 | 70 | 228 | 2.6% | 1.3% |
| 13 | 5,259 | 144 | 49 | 73 | 265 | 2.7% | 1.4% |
| 14 | 4,940 | 141 | 80 | 76 | 297 | 2.9% | 1.5% |
| 15+ | 13,549 | 416 | 298 | 276 | 990 | 3.1% | 2.0% |
| Total | 112,819 | 2,225 | 441 | 3,583 | 6,249 | 2.0% | 2.2% |
Figure 3: LTC lapse example: Reflects assumed mortality based on GAM 94 mortality table (unadjusted for duration/age trends)
Figures 4 and 5 show the results of a lapse study in which the assumed mortality has been adjusted using underwriting selection and durational factors as well as attained age adjustments that we see developed from studies of large LTC blocks of business. It also uses a more recent industry mortality table (Annuity 2000 Basic).
Figure 4: Long-term care lapse example Generic lapse study Annuity 2000 basic mortality table with selection factors and attained age adjustments
| Duration | Exposure | Expected deaths | Benefit exhaustion | Implied lapse | Total termination |
Results Mortality rate |
Resulting lapse rate |
| 1 | 10,000 | 48 | 0 | 681 | 729 | 0.5% | 6.8% |
| 2 | 9,307 | 77 | 0 | 586 | 663 | 0.8% | 6.3% |
| 3 | 8,623 | 87 | 0 | 497 | 585 | 1.0% | 5.8% |
| 4 | 8,183 | 95 | 0 | 378 | 473 | 1.2% | 4.6% |
| 5 | 7,785 | 102 | 0 | 322 | 425 | 1.3% | 4.1% |
| 6 | 7,430 | 106 | 0 | 248 | 354 | 1.4% | 3.3% |
| 7 | 7,086 | 113 | 0 | 204 | 317 | 1.6% | 2.9% |
| 8 | 6,721 | 118 | 0 | 156 | 274 | 1.8% | 2.3% |
| 9 | 6,418 | 140 | 0 | 84 | 224 | 2.2% | 1.3% |
| 10 | 6,143 | 149 | 0 | 62 | 211 | 2.4% | 1.0% |
| 11 | 5,831 | 155 | 0 | 61 | 216 | 2.7% | 1.0% |
| 12 | 5,543 | 161 | 13 | 54 | 228 | 2.9% | 1.0% |
| 13 | 5,259 | 164 | 49 | 52 | 265 | 3.1% | 1.0% |
| 14 | 4,940 | 168 | 80 | 49 | 297 | 3.4% | 1.0% |
| 15+ | 13,549 | 556 | 298 | 136 | 990 | 4.1% | 1.0% |
| Total | 112,819 | 2,240 | 441 | 3,568 | 6,249 | 2.0% | 2.2% |
Figure 5: LTC lapse example: Reflects Annuity 2000 basic mortality table with appropriate durational/attained age fit
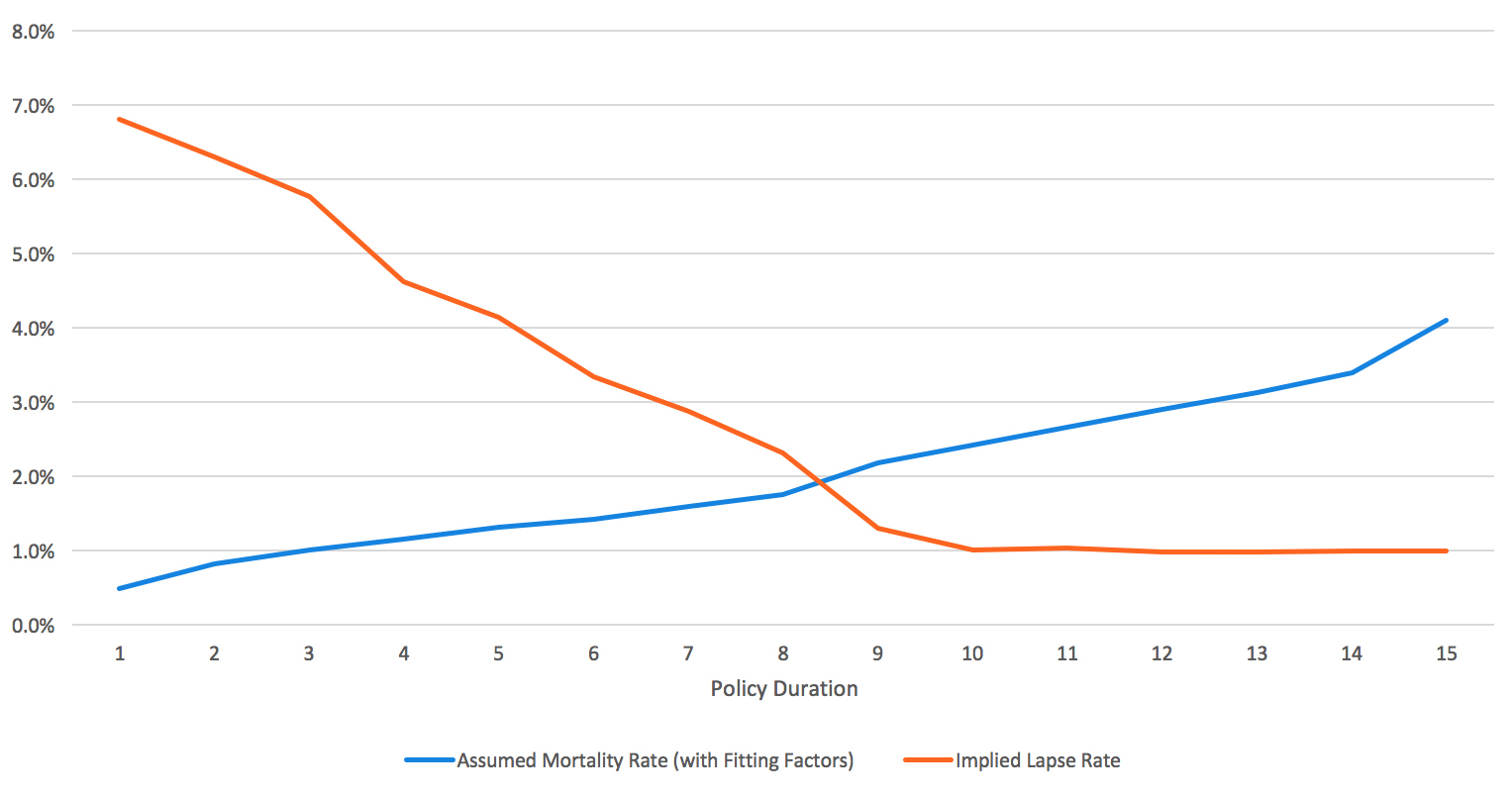
Figures 4 and 5 show smoother resulting implied lapse rates. Implied lapse rates decrease by duration through policy year 10, and then appear to reach a stable ultimate rate thereafter. This result is achieved through a few simple adjustments to mortality to reflect industry trends by duration and age.
It is important to note that, in aggregate across all durations, Figures 2 and 4 above have nearly identical expected deaths. Figure 2 shows 2,225 expected deaths, which is 2.0% of total exposures. Figure 4 shows 2,240 expected deaths, which is also 2.0% of total exposures. The surprising lapse rates that result in Figures 2 and 3 are, therefore, not a result of misstated mortality in aggregate. They are caused only by omission of important trends in durational and attained age mortality. This underscores the importance of carefully considering trends in mortality experience. Where credible company-specific mortality experience exists, it could be used for this purpose. Where it does not, it may be appropriate to supplement the persistency study with data available from industry studies.
Other considerations in lapse studies
There are several other considerations when conducting a lapse study in addition to the nuances related to developing healthy life lapse rates:
- Accurate measurement of deaths: As discussed earlier, it is critical in any lapse study to accurately measure deaths. Underreporting of deaths will overstate observed lapses. This will likely cause a skew in the results by age as there are more deaths at the older ages. An increasing pattern of lapses by age may mean that deaths are not being accurately measured.
- Impact of rate increases: There are several different items that need to be considered when evaluating lapse rates while rate increases are occurring. First, lapse rates will likely increase because of rate increases. This is commonly referred to as shock lapse. Separating the experience between those policies that are subject to rate increase and those that are not is important. Second, some policies that lapse go on to nonforfeiture status. Being able to separately track these policies will ensure that the underlying lapse rate can be measured appropriately and without influence. Depending on the purpose of the model, the lapse rate may need to reflect lapses in absence of rate increases (i.e., no shock lapses or policies going on to nonforfeiture status). Policies that are paid up on nonforfeiture status also affect other studies, such as mortality or morbidity. As the number of policies on nonforfeiture increases over time, experience studies will need to appropriately account for them.
- Benefit reductions: A similar assumption to lapse is how many people will reduce benefits as a result of a rate increase. This can be thought of as a partial lapse. As benefit reduction options and landing spots are becoming more popular, developing an assumption as to how many people elect benefit reductions is needed to have more accurate projections. Lapse studies may incorporate different metrics to study benefit reductions.
- Benefit exhaustions: In most first principles models, policies that go on claim and exhaust benefits will be calculated directly by the model. Therefore, the lapse rate assumption needs to represent voluntary lapses and exclude a termination that is due to exhausting benefits. It is important to accurately identify benefit exhaustions and remove them as a decrement from the study. Because benefit exhaustions tend to occur at the older ages, if they are not properly identified they could skew the lapse results by age.
- Other product features: Other product features commonly found in LTC plans, such as limited premium payment options and survivorship benefits, require special consideration in developing lapse assumptions.